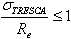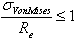Failure Criteria | |||||
|
| ||||
Failure Criteria for Composite Properties
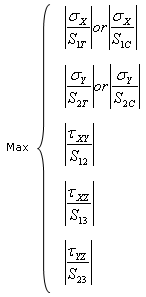
In a composite context with an orthotropic material (orthotropic 2D, orthotropic 3D, or fiber), you can compute failure criteria and visualize them as post-processing results. The failure criteria are Tsai-Hill, Tsai-Wu, Maximum Failure and Hoffman.
The characteristics of orthotropic materials are defined in the ELFINI Linear Elastic Domain dialog box. See Modifying ELFINI Linear Elastic Material Properties.
- Tensile stress limit X corresponds to the ultimate stress in tension along the X direction (S1T).
- Compressive stress limit X corresponds to the ultimate stress in compression along the X direction (S1C).
- Tensile stress limit Y corresponds to the ultimate stress in tension along the Y direction (S2T).
- Compressive stress limit Y corresponds to the ultimate stress in compression along the Y direction (S2C).
- Shear stress limit XY corresponds to the ultimate shear stress in the XY-plane (S12).
- Shear stress limit XZ corresponds to the ultimate shear stress in the XZ-plane (S13).
- Shear stress limit YZ corresponds to the ultimate shear stress in the YZ-plane (S23).
To learn more about the characteristics of orthotropic materials, see .
Tsai-Hill
ELFINI Linear Elastic Material PropertiesFor each lamina, the Tsai-Hill failure criterion requires that: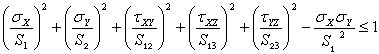
where:
- S1 = S1C if
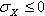
- S1 = S1T if
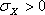
- S2 = S2C if
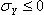
- S2 = S2T if
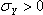
- For the
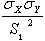 term: if
term: if 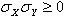 , S1 = S1T; otherwise S1 = S1C
, S1 = S1T; otherwise S1 = S1C
Special Cases
If one of the shear stress values (Shear stress limit XY, Shear stress limit YZ, or Shear stress limit XZ) is not defined in the ELFINI Linear Elastic Domain dialog box, the associated term is neglected in the formula (S12, S23 and S13 cannot be null in the formula).
For example, if you enter 0 as Shear stress limit XY value (S12=0) in the ELFINI Linear Elastic Domain dialog box, the Tsai-Hill failure criteria requires that: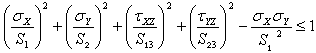
This means that the shear stresses in the XY-plane are neglected.
The formulas are different depending on:
- Material type:
- Fiber materials: the shear stress values in the YZ-plane and in the XZ-plane are equal (S23 = S13).
- Orthotropic 2D materials: terms associated to the Z-plane are neglected in the Tsai-Hill and Tsai-Wu formulas.
- Orthotropic 3D materials: all terms can be considered in the formulas.
- Finite element physical type:
- Shell: all terms can be considered in the formulas.
- Membrane: terms associated to the Z-plane are considered as null in the formulas.
- Shear Panel: only shear effects in the XY-plane are taken into account in the formulas.
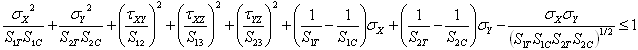
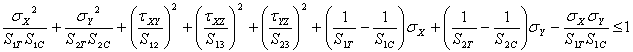
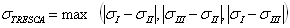
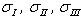 are the principal stresses.
are the principal stresses.