ELFINI Linear Elastic Material Properties | ||||
|
| |||
Isotropic
An isotropic material is defined with the following physical characteristics:
- Young's modulus
- Poisson's ratio
- Density
- Yield strength
- Coefficient of thermal expansion
An isotropic material is valid only if the following condition is satisfied: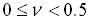
where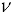 
is the Poisson's ratio.
Orthotropic 3D
An orthotropic 3D material is defined with the following physical characteristics:
- Young's modulus X
- Young's modulus Y
- Young's modulus Z
- Poisson's ratio XY
- Poisson's ratio XZ
- Poisson's ratio YZ
- Shear modulus XY
- Shear modulus XZ
- Shear modulus YZ
- Density
- Tensile stress limit X
- Compressive stress limit X
- Tensile stress limit Y
- Compressive stress limit Y
- Tensile stress limit Z
- Compressive stress limit Z
- Shear stress limit XY
- Shear stress limit XZ
- Shear stress limit YZ
- Coefficient of thermal expansion X
- Coefficient of thermal expansion Y
- Coefficient of thermal expansion Z
An orthotropic 3D material is valid only if the following
conditions are satisfied: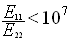
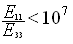
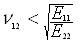
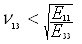
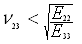
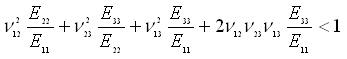
where:
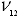is the Poisson's ratio that characterizes the transverse strain in
the Y-direction, when the material is stressed in the X-direction
(Poisson's ratio XY in the dialog box).
is the Poisson's ratio that characterizes the transverse strain in
the Z-direction, when the material is stressed in the X-direction
(Poisson's ratio XZ in the dialog box).
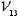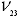is the Poisson's ratio that characterizes the transverse strain in
the Z-direction, when the material is stressed in the Y-direction
(Poisson's ratio YZ in the dialog box).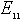
is the longitudinal Young's modulus (Young's modulus X in the dialog box).
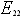is the transverse Young's modulus (Young's modulus Y in the dialog box).
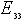is the normal Young's modulus (Young's modulus Z in the dialog box).
Orthotropic 2D
An orthotropic 2D material is defined with the following physical characteristics:
- Young's modulus X
- Young's modulus Y
- Poisson's ratio XY
- Shear modulus XY
- Shear modulus XZ
- Shear modulus YZ
- Density
- Tensile stress limit X
- Compressive stress limit X
- Tensile stress limit Y
- Compressive stress limit Y
- Shear stress limit XY
- Shear stress limit XZ
- Shear stress limit YZ
- Coefficient of thermal expansion X
- Coefficient of thermal expansion Y
An orthotropic 2D material is valid only if the following
conditions are satisfied: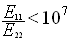
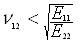
where:
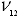- is the Poisson's ratio that characterizes the transverse strain in
the Y-direction, when the material is stressed in the X-direction
(Poisson's ratio XY in the dialog box).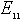
- is the longitudinal Young's modulus (Young's modulus X in the dialog box).
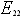- is the transverse Young's modulus (Young's modulus Y in the dialog box).
Fiber
A fiber material is defined with the following physical characteristics:
- Young's modulus X
- Young's modulus Y
- Poisson's ratio XY
- Shear modulus XY
- Shear modulus YZ
- Density
- Tensile stress limit X
- Compressive stress limit X
- Tensile stress limit Y
- Compressive stress limit Y
- Shear stress limit XY
- Shear stress limit YZ
- Coefficient of thermal expansion X
- Coefficient of thermal expansion Y
A fiber material is valid if the following condition is satisfied: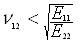
where:
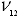- is the Poisson's ratio that characterizes the transverse strain in
the Y-direction, when the material is stressed in the X-direction
(Poisson's ratio XY in the dialog box).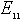
- is the longitudinal Young's modulus (Young's modulus X in the dialog box).
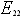- is the transverse Young's modulus (Young's modulus Y in the dialog box).