About Solver Computation | ||||||
|
| |||||
Element Stresses
This section gives you details about how the element stresses are computed.
Element stresses at Gauss points are the product of the
Comportment Law and the Strain Deformation.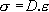
where:
-
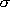 is
the element stress.
is
the element stress. 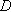 is
the Comportment Law, computed as a function of the following parameters,
where:
is
the Comportment Law, computed as a function of the following parameters,
where: is
the Poisson's ratio.
is
the Poisson's ratio.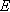 is
the Young's modulus.
is
the Young's modulus. is
the strain deformation, computed according to the displacement.
is
the strain deformation, computed according to the displacement.For example, with a 2D displacement:
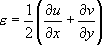
where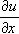 and
and 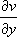 are the two partial derivatives.
are the two partial derivatives.
![]()
Node Stresses
This section gives you details about how the node stresses are computed.
Node stresses are extrapolations of element stresses. The method consists in defining a continuous stress field
within the element: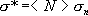
where:
-
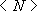 are
the element shape functions
are
the element shape functions -
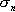 are
the node stresses to be computed
are
the node stresses to be computed
These nodal stresses values are obtained using the least
square minimization method: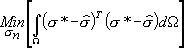
where 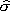 are the stresses computed with the finite element method from the nodal
displacements.
are the stresses computed with the finite element method from the nodal
displacements.
![]()
Contact Elements
This section gives you details about how contact elements are computed.
- It is assumed that contact property is non-linear (K.X = F(X)). Nevertheless, in the particular case of
contact without friction, the solution is unique: it does not
depend of the path used to put the two geometries in contact.
Static solutions inside the Structural Analysis product are thus solved with an iterative algorithm which could be qualified by an advanced linear approach. At each computation step, local contact directions are not updated (contrary to non-linear solvers). But if the local curvature is small (compared to contact area width), this approximation remains reliable and gives good results.
The contact connection mesh is done between overlapping surfaces at their initial position. The solver does not take into account large relative sliding between surfaces in contact. Contact condition is only valid for elements connected by the mesh.
- In case of contact with friction: after each contact iteration, the friction efforts are computed, and the contact computation is launched again.
- To solve contact problems, an additional stiffness is added to the
contact element.
Adding stiffness may influence displacements, especially in the
case of two solids that are not really in contact.
For example: consider two surfaces (S1 and S2) with 2mm distance between. Enforced displacements (dS1) are applied to S1: dS1 = -0.5mm
- Case 1: with no contact
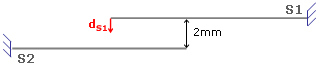
In this case, the displacements dS2 of the S2 surface are null: dS2 = 0mm.
- Case 2: with contact
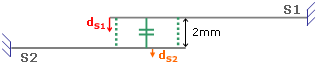
where symbolizes the contact elements.
symbolizes the contact elements.In this case dS2 is not equal to zero but the displacements are very small.
- Case 1: with no contact
![]()
Shell Elements
This section gives you details about how shell elements are computed.
The average normal vector is used for the computation of shell elements.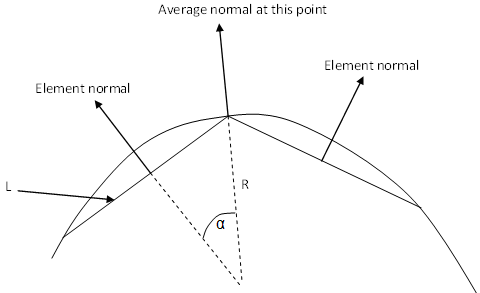
where:
- L is the element length.
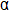 is the angle between the element normal and the average normal.
is the angle between the element normal and the average normal.- R is the estimated curvature radius
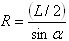
When the angle between the element normal and the average normal is smaller than the shell normal tolerance, and if the ratio between the curvature radius and the thickness is greater than two, the average normal is used instead of the element normal for all the shell elements (TR3, TR6, QD4, QD8). The default value of of the shell normal tolerance is 20 degrees, and its value can be set using the ELF_Shell_Normal_Tol environment variable. See Singularity Computation.