
Isotropic Plasticity
Isotropic plasticity is defined using a set of tabular data in which each row represents a True Plastic Strain value and the corresponding Yield Stress at that strain. Plastic strain to stress relationships are interpolated linearly between each provided data point; the stress remains constant at strains outside the specified data range.
| True Plastic Strain |
Plastic component of the true—or logarithmic—strain in the material (i.e., true strain that will not be recovered after the stress is removed). |
| Yield Stress |
True—or logarithmic—stress value at the corresponding true plastic strain. |

Viscoelastic
Viscoelastic behavior is defined numerically using a Prony series expansion of the shear and bulk relaxation moduli in the material. Data are entered in a table in which each row represents a set of constants in one term of the Prony series; the order of the rows corresponds to the order of the terms in the series.
| Gi Prony |
The modulus ratio in the corresponding term in the Prony series expansion
of the shear relaxation modulus.
|
| Ki Prony |
The modulus ratio in the corresponding term in the Prony series expansion
of the bulk relaxation modulus.
|
| Tau_i Prony |
The relaxation time, in units of seconds, for the corresponding term in the Prony series
expansion.
|

Damping
Material damping is specified according to the following equation:
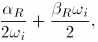
where 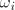 are the natural frequencies of the model on which the material is applied.
are the natural frequencies of the model on which the material is applied.
| Alpha |
The mass proportional damping factor; this factor tends to have a stronger effect at lower frequencies. |
| Beta |
The stiffness proportional damping factor; this factor tends to have a stronger effect at higher frequencies. |

Expansion
Isotropic thermal strains occur according to the following equation:
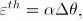
where 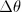 is the temperature change in the model.
is the temperature change in the model.
| Alpha |
The coefficient of thermal expansion. |
![]()
![]()
![]()
![]()
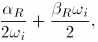
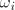 are the natural frequencies of the model on which the material is applied.
are the natural frequencies of the model on which the material is applied.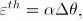
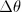 is the temperature change in the model.
is the temperature change in the model.