About Notations Used for Inertia Matrices

This section will help you read the information given in the Measure Inertia dialog box for Inertia Matrix / G, Inertia Matrix / O, Inertia Matrix / P and Inertia Matrix / Axis System A.

Moments and Products of 3D Inertia

Iox

Moment of inertia of the object about the ox axis:

Ioy

Moment of inertia of the object about the oy axis:

Ioz

Moment of inertia of the object about the oz axis:

Pxy

Product of inertia of the object about axes ox and oy:

Pxz

Product of inertia of the object about axes ox and oz:

Pyz

Product of inertia of the object about axes oy and oz:

(where M is the mass of the object; units: kg.m2)

Moments and Products of 2D Inertia

Iox

Moment of inertia of the surface about the ox axis:

Ioy

Moment of inertia of the surface about the oy axis:

Pxy

Product of inertia of the surface about axes ox and oy:

(where A is the surface; units: m4)

Matrix of Inertia

3D Inertia: 2D Inertia:




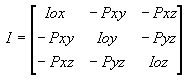where I is the matrix of inertia of the object with respect to orthonormal basis Oxyz

Moments and Principal Axes

The matrix of inertia being a real matrix (whose elements consist entirely of real numbers) and a symmetric matrix, there exists an orthonormal basis of vectors in this matrix of inertia.

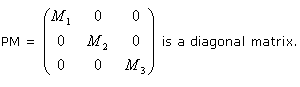
The principal axes are defined by vectors and inertia principal moments are expressed by



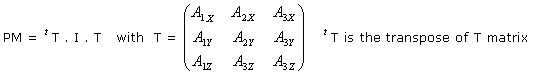
Note: is an orthonormal direct basis.

Expression in Any Axis System

I is the matrix of inertia with respect to orthonormal basis Oxyz.

Huygen's theorem is used to transform the matrix of inertia: (parallel axis theorem).

Let I' be the matrix of inertia with respect to orthonormal basis Pxyz where



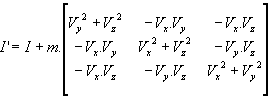
M = {u,v,w}: transformation matrix from basis (Pxyz) to basis (Puvw) TM is the transposed matrix of matrix M.

J is the matrix of inertia with respect to an orthonormal basis Puvw:

J = TM.I'.M

Additional Notation Used in the Measure Inertia Command

Ixy = (-Pxy)

Ixz = (-Pxz)

Iyz = (-Pyz)

Note: Since entries for the opposite of the product are symmetrical, they are given only once in the dialog box.

IoxG

Moment of inertia of the object about the ox axis with respect to the system Gxyz, where G is the center of gravity.

IoxO

Moment of inertia of the object about the ox axis with respect to the system Oxyz, where O is the origin of the document.

IoxP

Moment of inertia of the object about the ox axis with respect to the system Pxyz, where P is a selected point.

IoxA

Moment of inertia of the object about the ox axis with respect to the system Axyz, where A is a selected axis system.

etc.