Creating Conic Curves

You can create conics. Conic curves are the curves defined by five constraints: start and end points, passing points or tangents. The resulting curves are arcs of parabolas, hyperbolas or ellipses.

The different elements necessary to define these curves are either:


  • two points, start and end tangents, and a parameter
  • two points, start and end tangents, and a passing point
  • two points, a tangent intersection point, and a parameter
  • two points, a tangent intersection point, and a passing point
  • four points and a tangent
  • five points

Before you begin: Create a 3D shape containing at least two points.

  1. Click Conic in the Wireframe toolbar (Circle-Conic sub-toolbar).

    The Conic Definition dialog box appears.

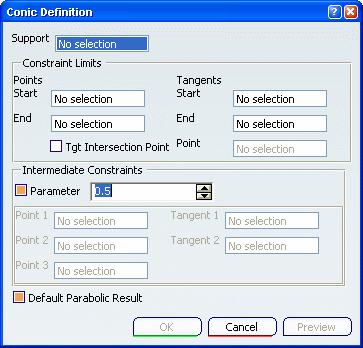
  2. In the Support box, select the plane on which the resulting curve will lie.

  3. Fill in the conic curve parameters, depending on the type of curve to be created by selecting geometric elements (points, lines, etc.).


    • Start and End points: the curve is defined from the starting point to the end point.
    • Tangents Start and End: if necessary, the tangent at the starting or end point defined by selecting a line.

    Selecting the support plane and starting point

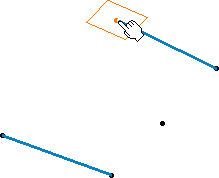
    Selecting the ending point

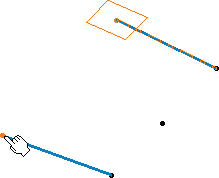
    Selecting the tangent at the starting point

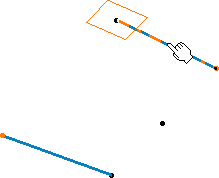
    Selecting the tangent at the ending point

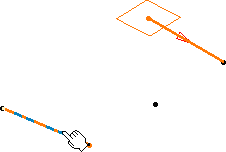
    Resulting conic curve


    • Tgt Intersection Point: a point used to define directly both tangents from the start and end point. These tangents are created on the virtual lines passing through the start (end) point and the selected point.

    Using a tangent intersection point

    Resulting conic curve

  4. Clear the Default Parabolic Result box () if you do not want the resulting conic curve to be parabolic.

    By default, it is selected.

  5. Click OK to create the conic curve.

    The conic curve (identified as Conic.xxx) is added to the specification tree.

    Note: Intermediate Constraints:

    • Point 1, 2, 3: possible passing points for the curve. These points have to be selected in logical order, that is the curve will pass through the start point, then through Point 1, Point 2, Point 3 and the end point.

      Depending on the type of curve, not all three points have to be selected.

      You can define tangents on Point 1 and Point 2 (Tangent 1 or 2).
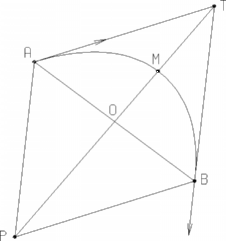
    • Parameter: ratio ranging from 0 to 1 (excluded), this value is used to define a passing point (M in the figure below) and corresponds to the OM distance/OT distance.

      If parameter = 0.5, the resulting curve is a parabola If 0 < parameter < 0.5, the resulting curve is an arc of ellipse, If 1 > parameter > 0.5, the resulting curve is a hyperbola.